Temporal Networks¶

epipack provides a tiny interface to simulate StochasticEpiModels on temporal networks, see epipack.temporal_networks. Note that such simulations are based on the simulation routine for static networks and therefore numerically correct but not particularly efficient (the event set is reset in its entirety every time the network structure changes).

The idea is once again that prototyping should be fast, i.e. building new models in a flexible manner, leaving simulation efficiency aside.

Standard epipdemiological models are implemented in tacoma which you should use if you want to go for fast simulations.

Temporal Network Objects¶

A temporal network is defined by the following properties

N: the constant number of nodes in the system
t: A sorted list containing each time point at which the edge set will be updated
tmax: A final time that marks the end of the experiment (not associated with an edge set update).

edges: An ordered list of edge sets.

edges = [
    [ (0,1), ... ], # edge set for first timestamp
    [ (2,7), ... ], # edge set for second timestamp
    ...
]

directed: boolean, whether or not edges in edge set are supposed to be symmetric

weighted: boolean, if True, the edges in the edge sets per time stamp are expected to be 3-tuples where the last entry is a float value

edges = [
    [ (0,1,1.0), ... ], # edge set for first timestamp
    [ (2,7,0.5), ... ], # edge set for second timestamp
    ...
]

This is a variant of how temporal networks are defined in tacoma (in tacoma, more temporal network types are possible, but every one of them only offers unweighted and undirected edges).

In epipack, temporal networks are supposed to be constructed using the epipack.temporal_networks.TemporalNetwork class.

Here's an example:

edges = [ [ (0,1) ], [ (0,1), (0,2) ], [] ]
t = [0,0.5,1.5]
temporal_network = TemporalNetwork(N=3,edge_lists=edges,t=t,tmax=3.0)

Now we can iterate through the network:

for this_edge_list, this_t, next_t in temporal_network:
    if this_t >= 12:
        break
    print("t in [",this_t, next_t,"], edges:", this_edge_list)

And this is the outcome:

t in [ 0 0.5 ], edges: [(0, 1, 1.0)]
t in [ 0.5 1.5 ], edges: [(0, 1, 1.0), (0, 2, 1.0)]
t in [ 1.5 3.0 ], edges: []
t in [ 3.0 3.5 ], edges: [(0, 1, 1.0)]
t in [ 3.5 4.5 ], edges: [(0, 1, 1.0), (0, 2, 1.0)]
t in [ 4.5 6.0 ], edges: []
t in [ 6.0 6.5 ], edges: [(0, 1, 1.0)]
t in [ 6.5 7.5 ], edges: [(0, 1, 1.0), (0, 2, 1.0)]
t in [ 7.5 9.0 ], edges: []
t in [ 9.0 9.5 ], edges: [(0, 1, 1.0)]
t in [ 9.5 10.5 ], edges: [(0, 1, 1.0), (0, 2, 1.0)]
t in [ 10.5 12.0 ], edges: []

Two things can be noticed immediately. First, a default edge weight of 1.0 is added to every node pair of the originally unweighted network. This is done because StochasticEpiModel expects weighted edge tuples. Second, temporal networks are looped indefinitely per default, which is why we have to break the loop manually. If you don't want them to loop but to stop the simulation at tmax, pass the keyword loop_network=False to the constructor

TemporalNetwork(loop_network=False,*args,**kwargs)

The mean out degree is important to determine how fast a virus can spread through the network. You can obtain its value using the method mean_out_degree().

k_out = temporal_network.mean_out_degree()

Construct Temporal Networks with Tacoma¶

tacoma offers an extensive temporal network analysis frame work, such that it makes sense to use it to load temporal networks. For instance:

tn = tc.load_json_taco("~/.tacoma/hs13.taco")
tn = TemporalNetwork.from_tacoma(tn)

Simulate with StochasticEpiModel¶

After loading a temporal network, set up a simulation using epipack.temporal_networks.TemporalNetworkSimulation.

First, let's load a temporal network and define a simple SIR model.

# load network
tn = tc.load_json_taco("~/.tacoma/hs13.taco")
tn = TemporalNetwork.from_tacoma(tn)

# compute disease parameters
k = tn.mean_out_degree()
R0 = 2.0
recovery_rate = 1/(2*24*3600)
infection_rate = R0 * recovery_rate / k

# define model
model = StochasticEpiModel(['S','I','R'],N=tn.N)\
            .set_node_transition_processes([
                ('I', recovery_rate, 'R')
            ])\
            .set_link_transmission_processes([
                ('I', 'S', infection_rate, 'I', 'I')
            ])\
            .set_random_initial_conditions({
                'S': tn.N - 10,
                'I': 10
            })

Now, we can set up a simulation object and simulate the whole thing.

sim = TemporalNetworkSimulation(tn, model)
t, result = sim.simulate(tmax=2*7*24*3600)

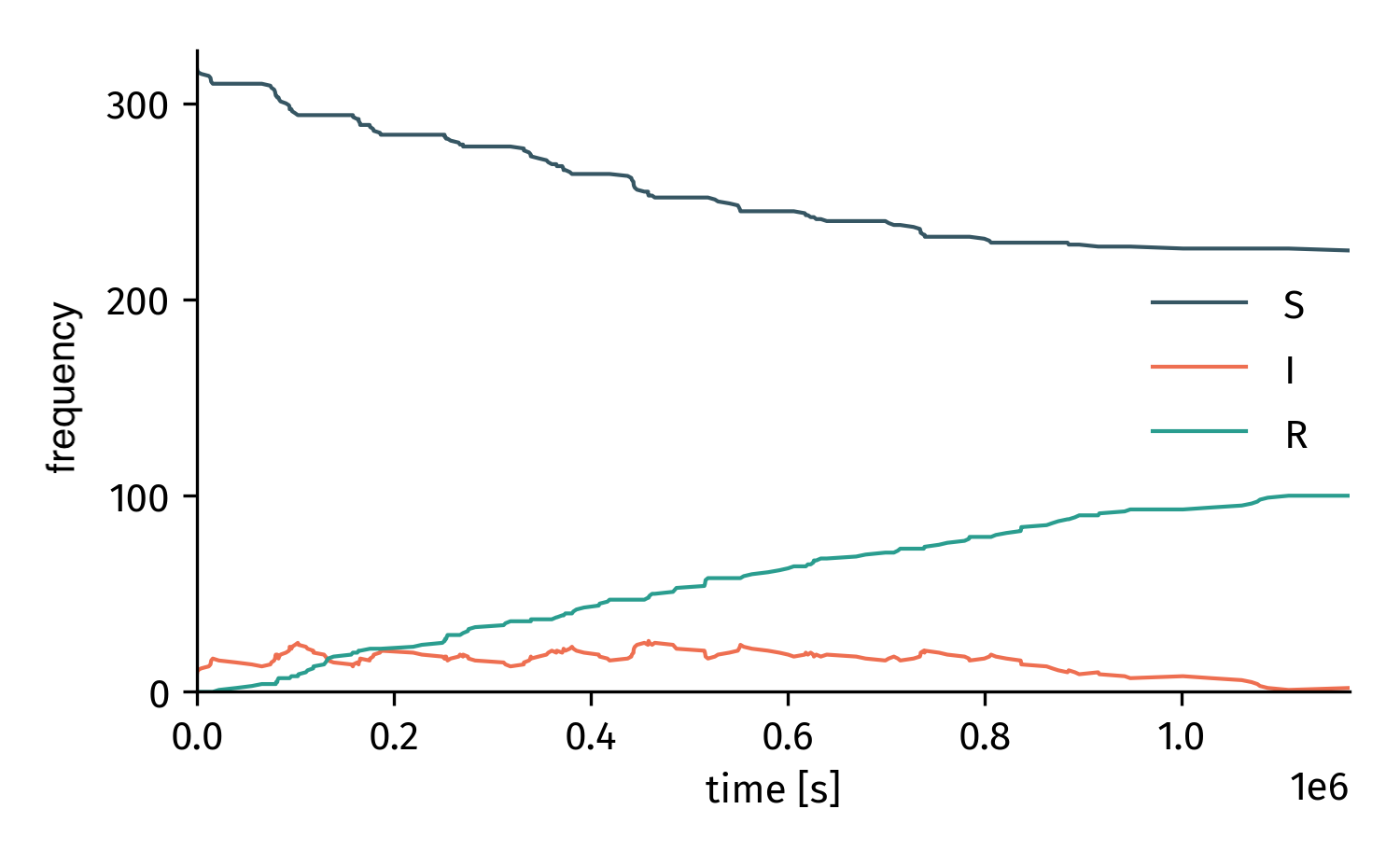
Stochastic simulation on a temporal network.¶